Magic Squares of Odd Order

Magic Squares of odd order

Magic Squares of odd order by Marios Mamzeris

This page presents the Mamzeris Method: a systematic approach to constructing associative magic squares of any odd order using simple two-pass transformations or direct mathematical formulas.

The Origin Story

I developed this method in 1988 while studying computer science. When my university's mathematics faculty presented what they called an 'unsolved problem' in magic square construction, they challenged me to apply my programming background to find a systematic solution. What emerged was a universal algorithmic method that works for any odd-order magic square. I used this method personally for over three decades before publishing it in 2020, along with a new universal closed-form formula that enables direct calculation of any cell position.

A Magic Square is an n × n square grid (where n is the number of cells on each side) filled with distinct positive integers in the range 1,2,...,n² such that each cell contains a different integer and the sum of integers in each row, column, and diagonal is equal.

An associative magic square has an elegant property: pairs of numbers positioned symmetrically opposite the centre always sum to n² + 1. For example, in a 7×7 square (n²=49), opposite pairs sum to 50. These are also called symmetric magic squares, and all associative magic squares are self-complementary. (Wikipedia)

The Mamzeris Method offers two complementary approaches:

1. Algorithmic Construction (detailed below): A two-pass table transformation using row and column shifts. Best for learning, teaching, or manual construction.

2. Universal Closed-Form Formula: A direct mathematical formula that computes the value of any cell position (x, y) for any odd order N. This formula, published in 2025, enables instant calculation without iterative steps. Best for programming, large squares, or individual cell calculations. View the complete mathematical formula

Algorithmic Construction Method:

To create any odd-order associative magic square quickly and efficiently using the algorithmic approach, we need to perform only two simple passes, which I call table transformations (shifts). The three tables below demonstrate the construction of a 31×31 magic square.

Pass 1: Begin with a table filled sequentially with all numbers from 1 to n² (1^st table below, with cells shifting shown in green). Perform a left shift of all rows, skipping the middle one: shift the first row by one cell, the second row by two cells, and so on, until the last (n^th) row is shifted by n−1 cells.

Pass 2: Apply a similar transformation to columns instead of rows. Shift cells upward, starting with one cell in the leftmost column, two cells in the next column, and so on, until the last (n^th) column is shifted by n−1 cells, skipping the middle column. This is shown in the 2^nd table below with cells shifting in blue.

That's it. A magic square is ready. The completed square is shown in the 3^rd table below, with alternating grey cells and highlighted yellow diagonals.

1. Initial Table: Begin with numbers from 1 to n² arranged sequentially
The green arrow indicates the direction of the upcoming cell shift. Green-highlighted cells show which cells will move.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
1		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
2		32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62
3		63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93
4		94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124
5		125	126	127	128	129	130	131	132	133	134	135	136	137	138	139	140	141	142	143	144	145	146	147	148	149	150	151	152	153	154	155
6		156	157	158	159	160	161	162	163	164	165	166	167	168	169	170	171	172	173	174	175	176	177	178	179	180	181	182	183	184	185	186
7		187	188	189	190	191	192	193	194	195	196	197	198	199	200	201	202	203	204	205	206	207	208	209	210	211	212	213	214	215	216	217
8		218	219	220	221	222	223	224	225	226	227	228	229	230	231	232	233	234	235	236	237	238	239	240	241	242	243	244	245	246	247	248
9		249	250	251	252	253	254	255	256	257	258	259	260	261	262	263	264	265	266	267	268	269	270	271	272	273	274	275	276	277	278	279
10		280	281	282	283	284	285	286	287	288	289	290	291	292	293	294	295	296	297	298	299	300	301	302	303	304	305	306	307	308	309	310
11		311	312	313	314	315	316	317	318	319	320	321	322	323	324	325	326	327	328	329	330	331	332	333	334	335	336	337	338	339	340	341
12		342	343	344	345	346	347	348	349	350	351	352	353	354	355	356	357	358	359	360	361	362	363	364	365	366	367	368	369	370	371	372
13		373	374	375	376	377	378	379	380	381	382	383	384	385	386	387	388	389	390	391	392	393	394	395	396	397	398	399	400	401	402	403
14		404	405	406	407	408	409	410	411	412	413	414	415	416	417	418	419	420	421	422	423	424	425	426	427	428	429	430	431	432	433	434
15		435	436	437	438	439	440	441	442	443	444	445	446	447	448	449	450	451	452	453	454	455	456	457	458	459	460	461	462	463	464	465
16		466	467	468	469	470	471	472	473	474	475	476	477	478	479	480	481	482	483	484	485	486	487	488	489	490	491	492	493	494	495	496
17		497	498	499	500	501	502	503	504	505	506	507	508	509	510	511	512	513	514	515	516	517	518	519	520	521	522	523	524	525	526	527
18		528	529	530	531	532	533	534	535	536	537	538	539	540	541	542	543	544	545	546	547	548	549	550	551	552	553	554	555	556	557	558
19		559	560	561	562	563	564	565	566	567	568	569	570	571	572	573	574	575	576	577	578	579	580	581	582	583	584	585	586	587	588	589
20		590	591	592	593	594	595	596	597	598	599	600	601	602	603	604	605	606	607	608	609	610	611	612	613	614	615	616	617	618	619	620
21		621	622	623	624	625	626	627	628	629	630	631	632	633	634	635	636	637	638	639	640	641	642	643	644	645	646	647	648	649	650	651
22		652	653	654	655	656	657	658	659	660	661	662	663	664	665	666	667	668	669	670	671	672	673	674	675	676	677	678	679	680	681	682
23		683	684	685	686	687	688	689	690	691	692	693	694	695	696	697	698	699	700	701	702	703	704	705	706	707	708	709	710	711	712	713
24		714	715	716	717	718	719	720	721	722	723	724	725	726	727	728	729	730	731	732	733	734	735	736	737	738	739	740	741	742	743	744
25		745	746	747	748	749	750	751	752	753	754	755	756	757	758	759	760	761	762	763	764	765	766	767	768	769	770	771	772	773	774	775
26		776	777	778	779	780	781	782	783	784	785	786	787	788	789	790	791	792	793	794	795	796	797	798	799	800	801	802	803	804	805	806
27		807	808	809	810	811	812	813	814	815	816	817	818	819	820	821	822	823	824	825	826	827	828	829	830	831	832	833	834	835	836	837
28		838	839	840	841	842	843	844	845	846	847	848	849	850	851	852	853	854	855	856	857	858	859	860	861	862	863	864	865	866	867	868
29		869	870	871	872	873	874	875	876	877	878	879	880	881	882	883	884	885	886	887	888	889	890	891	892	893	894	895	896	897	898	899
30		900	901	902	903	904	905	906	907	908	909	910	911	912	913	914	915	916	917	918	919	920	921	922	923	924	925	926	927	928	929	930
31		931	932	933	934	935	936	937	938	939	940	941	942	943	944	945	946	947	948	949	950	951	952	953	954	955	956	957	958	959	960	961

 

2. After First Pass: Rows shifted, columns ready for transformation
The blue arrow indicates the direction of the second shift. Blue-highlighted cells show which cells will move.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
1		2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	1
2		34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	32	33
3		66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	63	64	65
4		98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	94	95	96	97
5		130	131	132	133	134	135	136	137	138	139	140	141	142	143	144	145	146	147	148	149	150	151	152	153	154	155	125	126	127	128	129
6		162	163	164	165	166	167	168	169	170	171	172	173	174	175	176	177	178	179	180	181	182	183	184	185	186	156	157	158	159	160	161
7		194	195	196	197	198	199	200	201	202	203	204	205	206	207	208	209	210	211	212	213	214	215	216	217	187	188	189	190	191	192	193
8		226	227	228	229	230	231	232	233	234	235	236	237	238	239	240	241	242	243	244	245	246	247	248	218	219	220	221	222	223	224	225
9		258	259	260	261	262	263	264	265	266	267	268	269	270	271	272	273	274	275	276	277	278	279	249	250	251	252	253	254	255	256	257
10		290	291	292	293	294	295	296	297	298	299	300	301	302	303	304	305	306	307	308	309	310	280	281	282	283	284	285	286	287	288	289
11		322	323	324	325	326	327	328	329	330	331	332	333	334	335	336	337	338	339	340	341	311	312	313	314	315	316	317	318	319	320	321
12		354	355	356	357	358	359	360	361	362	363	364	365	366	367	368	369	370	371	372	342	343	344	345	346	347	348	349	350	351	352	353
13		386	387	388	389	390	391	392	393	394	395	396	397	398	399	400	401	402	403	373	374	375	376	377	378	379	380	381	382	383	384	385
14		418	419	420	421	422	423	424	425	426	427	428	429	430	431	432	433	434	404	405	406	407	408	409	410	411	412	413	414	415	416	417
15		450	451	452	453	454	455	456	457	458	459	460	461	462	463	464	465	435	436	437	438	439	440	441	442	443	444	445	446	447	448	449
16		466	467	468	469	470	471	472	473	474	475	476	477	478	479	480	481	482	483	484	485	486	487	488	489	490	491	492	493	494	495	496
17		513	514	515	516	517	518	519	520	521	522	523	524	525	526	527	497	498	499	500	501	502	503	504	505	506	507	508	509	510	511	512
18		545	546	547	548	549	550	551	552	553	554	555	556	557	558	528	529	530	531	532	533	534	535	536	537	538	539	540	541	542	543	544
19		577	578	579	580	581	582	583	584	585	586	587	588	589	559	560	561	562	563	564	565	566	567	568	569	570	571	572	573	574	575	576
20		609	610	611	612	613	614	615	616	617	618	619	620	590	591	592	593	594	595	596	597	598	599	600	601	602	603	604	605	606	607	608
21		641	642	643	644	645	646	647	648	649	650	651	621	622	623	624	625	626	627	628	629	630	631	632	633	634	635	636	637	638	639	640
22		673	674	675	676	677	678	679	680	681	682	652	653	654	655	656	657	658	659	660	661	662	663	664	665	666	667	668	669	670	671	672
23		705	706	707	708	709	710	711	712	713	683	684	685	686	687	688	689	690	691	692	693	694	695	696	697	698	699	700	701	702	703	704
24		737	738	739	740	741	742	743	744	714	715	716	717	718	719	720	721	722	723	724	725	726	727	728	729	730	731	732	733	734	735	736
25		769	770	771	772	773	774	775	745	746	747	748	749	750	751	752	753	754	755	756	757	758	759	760	761	762	763	764	765	766	767	768
26		801	802	803	804	805	806	776	777	778	779	780	781	782	783	784	785	786	787	788	789	790	791	792	793	794	795	796	797	798	799	800
27		833	834	835	836	837	807	808	809	810	811	812	813	814	815	816	817	818	819	820	821	822	823	824	825	826	827	828	829	830	831	832
28		865	866	867	868	838	839	840	841	842	843	844	845	846	847	848	849	850	851	852	853	854	855	856	857	858	859	860	861	862	863	864
29		897	898	899	869	870	871	872	873	874	875	876	877	878	879	880	881	882	883	884	885	886	887	888	889	890	891	892	893	894	895	896
30		929	930	900	901	902	903	904	905	906	907	908	909	910	911	912	913	914	915	916	917	918	919	920	921	922	923	924	925	926	927	928
31		961	931	932	933	934	935	936	937	938	939	940	941	942	943	944	945	946	947	948	949	950	951	952	953	954	955	956	957	958	959	960

 

3. Completed Magic Square: Final result after both transformations
All rows, columns, and diagonals now sum to the magic constant. Grey cells alternate for visibility, and yellow highlights show the main diagonals.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
1		34	67	100	133	166	199	232	265	298	331	364	397	430	463	480	17	498	531	564	597	630	663	696	729	762	795	828	861	894	927	960
2		66	99	132	165	198	231	264	297	330	363	396	429	462	479	527	49	530	563	596	629	662	695	728	761	794	827	860	893	926	959	1
3		98	131	164	197	230	263	296	329	362	395	428	461	478	526	528	81	562	595	628	661	694	727	760	793	826	859	892	925	958	31	33
4		130	163	196	229	262	295	328	361	394	427	460	477	525	558	560	113	594	627	660	693	726	759	792	825	858	891	924	957	30	32	65
5		162	195	228	261	294	327	360	393	426	459	476	524	557	559	592	145	626	659	692	725	758	791	824	857	890	923	956	29	62	64	97
6		194	227	260	293	326	359	392	425	458	475	523	556	589	591	624	177	658	691	724	757	790	823	856	889	922	955	28	61	63	96	129
7		226	259	292	325	358	391	424	457	474	522	555	588	590	623	656	209	690	723	756	789	822	855	888	921	954	27	60	93	95	128	161
8		258	291	324	357	390	423	456	473	521	554	587	620	622	655	688	241	722	755	788	821	854	887	920	953	26	59	92	94	127	160	193
9		290	323	356	389	422	455	472	520	553	586	619	621	654	687	720	273	754	787	820	853	886	919	952	25	58	91	124	126	159	192	225
10		322	355	388	421	454	471	519	552	585	618	651	653	686	719	752	305	786	819	852	885	918	951	24	57	90	123	125	158	191	224	257
11		354	387	420	453	470	518	551	584	617	650	652	685	718	751	784	337	818	851	884	917	950	23	56	89	122	155	157	190	223	256	289
12		386	419	452	469	517	550	583	616	649	682	684	717	750	783	816	369	850	883	916	949	22	55	88	121	154	156	189	222	255	288	321
13		418	451	468	516	549	582	615	648	681	683	716	749	782	815	848	401	882	915	948	21	54	87	120	153	186	188	221	254	287	320	353
14		450	467	515	548	581	614	647	680	713	715	748	781	814	847	880	433	914	947	20	53	86	119	152	185	187	220	253	286	319	352	385
15		466	514	547	580	613	646	679	712	714	747	780	813	846	879	912	465	946	19	52	85	118	151	184	217	219	252	285	318	351	384	417
16		513	546	579	612	645	678	711	744	746	779	812	845	878	911	944	481	18	51	84	117	150	183	216	218	251	284	317	350	383	416	449
17		545	578	611	644	677	710	743	745	778	811	844	877	910	943	16	497	50	83	116	149	182	215	248	250	283	316	349	382	415	448	496
18		577	610	643	676	709	742	775	777	810	843	876	909	942	15	48	529	82	115	148	181	214	247	249	282	315	348	381	414	447	495	512
19		609	642	675	708	741	774	776	809	842	875	908	941	14	47	80	561	114	147	180	213	246	279	281	314	347	380	413	446	494	511	544
20		641	674	707	740	773	806	808	841	874	907	940	13	46	79	112	593	146	179	212	245	278	280	313	346	379	412	445	493	510	543	576
21		673	706	739	772	805	807	840	873	906	939	12	45	78	111	144	625	178	211	244	277	310	312	345	378	411	444	492	509	542	575	608
22		705	738	771	804	837	839	872	905	938	11	44	77	110	143	176	657	210	243	276	309	311	344	377	410	443	491	508	541	574	607	640
23		737	770	803	836	838	871	904	937	10	43	76	109	142	175	208	689	242	275	308	341	343	376	409	442	490	507	540	573	606	639	672
24		769	802	835	868	870	903	936	9	42	75	108	141	174	207	240	721	274	307	340	342	375	408	441	489	506	539	572	605	638	671	704
25		801	834	867	869	902	935	8	41	74	107	140	173	206	239	272	753	306	339	372	374	407	440	488	505	538	571	604	637	670	703	736
26		833	866	899	901	934	7	40	73	106	139	172	205	238	271	304	785	338	371	373	406	439	487	504	537	570	603	636	669	702	735	768
27		865	898	900	933	6	39	72	105	138	171	204	237	270	303	336	817	370	403	405	438	486	503	536	569	602	635	668	701	734	767	800
28		897	930	932	5	38	71	104	137	170	203	236	269	302	335	368	849	402	404	437	485	502	535	568	601	634	667	700	733	766	799	832
29		929	931	4	37	70	103	136	169	202	235	268	301	334	367	400	881	434	436	484	501	534	567	600	633	666	699	732	765	798	831	864
30		961	3	36	69	102	135	168	201	234	267	300	333	366	399	432	913	435	483	500	533	566	599	632	665	698	731	764	797	830	863	896
31		2	35	68	101	134	167	200	233	266	299	332	365	398	431	464	945	482	499	532	565	598	631	664	697	730	763	796	829	862	895	928

 

---

Alternative Approach: Bidirectional Shifting

Instead of shifting all rows in one direction and all columns in another, you can shift each half of the table in opposite directions (always skipping the middle row or column). This produces the same result using a mirror-symmetry pattern.

Initial square with numbers 1 - n² in sequence

1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31	32	33	34	35
36	37	38	39	40	41	42
43	44	45	46	47	48	49

After the first pass: Notice how each column is equal to Σ

	2	3	4	5	6	7	1
	10	11	12	13	14	8	9
	18	19	20	21	15	16	17
	22	23	24	25	26	27	28
	33	34	35	29	30	31	32
	41	42	36	37	38	39	40
	49	43	44	45	46	47	48

 

Second pass completed: Now each row is also equal to Σ. The Magic Square is ready!

10	19	24	5	30	39	48
18	23	35	13	38	47	1
22	34	36	21	46	7	9
33	42	44	25	6	8	17
41	43	4	29	14	16	28
49	3	12	37	15	27	32
2	11	20	45	26	31	40

---

Universal Closed-Form Formula

In addition to the algorithmic construction method described above, the Mamzeris Method includes a universal closed-form formula that directly computes the value at any cell position without performing iterative shifts. This formula was published in my 2025 paper: Universal Closed-Form Construction for Odd-Order Magic Squares (The Mamzeris Method).

Key advantages of the closed-form formula:

• Direct computation: Calculate any individual cell value without constructing the entire square
• Computational efficiency: Ideal for programming, large squares, or sparse calculations
• Mathematical completeness: Provides explicit mathematical expression for the entire construction
• Validation tool: Verify algorithmic constructions or explore specific patterns

Formula notation (simplified overview):

For any odd order N ≥ 3, the value V(x, y) at cell position (x, y) is computed using modular arithmetic based on row and column shift functions. The complete formula with detailed notation, worked examples, and step-by-step calculations is available in the published paper.

Example calculation: For a 5×5 magic square, to find the value at position (3, 4):

• Using the formula: V(3, 4) = 16
• This matches the algorithmically constructed square shown above

The formula works for any odd-order magic square and produces results identical to the algorithmic method, providing two complementary ways to understand and generate these mathematical structures.

---

Understanding How the Method Works

This section explains the mathematical insight behind why the two-pass transformation creates a magic square of odd order. Understanding the balance of row and column sums reveals the elegance of the method.

Key Variables:

n = the square's dimension (for a 7×7 square, n = 7)
M = (n² + 1)/2 = the middle number (located at the center)
Σ = M×n = the magic constant (target sum for each row, column, and diagonal)
r = distance from the middle row or column

The Balancing Principle:

When we fill the initial square (1) with numbers 1 to n² in sequence, each row and column has a different sum based on its distance from the center. This creates predictable "weight" imbalances:

For columns:
• Moving left from center: each column's sum = Σ - r×n
• Moving right from center: each column's sum = Σ + r×n

For rows:
• Moving up from center: each row's sum = Σ - (r×n²)
• Moving down from center: each row's sum = Σ + (r×n²)

Pass 1 - Balancing the Rows:

The first pass shifts cells left by increasing amounts (row 1 shifts by 1, row 2 by 2, etc.), skipping the middle row. This creates square (2) where all row sums equal Σ.

The key insight: cells shifted off the left edge wrap to the right, adding exactly the right amount to compensate for each row's initial imbalance. The top row gains +1, the next gains +2, and so on, perfectly counterbalancing the initial deficits.

Pass 2 - Balancing the Columns:

The second pass applies the same logic to columns, shifting cells upward by increasing amounts. This transforms square (2) into square (3), where all column sums also equal Σ, creating a perfect magic square.

Visual Guide to the Tables Below:

Left tables: Show each cell's value relative to n (the algebraic view)
Right tables: Show actual numeric values as the square transforms
Green cells: Display row and column sums (diagonals always equal Σ)
Blue cells: Track the middle row and column positions through both passes
Square (3): The completed magic square with all properties satisfied

								Σ										175		Σ
n-6	n-5	n-4	n-3	n-2	n-1	n		Σ -(3n2)		1	2	3	4	5	6	7		28		Σ -(3n2)
n+1	n+2	n+3	n+4	n+5	n+6	n+7		Σ -(2n2)		8	9	10	11	12	13	14		77		Σ -(2n2)
n+8	n+9	n+10	n+11	n+12	n+13	n+14		Σ -(1n2)		15	16	17	18	19	20	21		126		Σ -(1n2)
n+15	n+16	n+17	n+18	n+19	n+20	n+21		Σ		22	23	24	25	26	27	28		175		Σ
n+22	n+23	n+24	n+25	n+26	n+27	n+28		Σ +(1n2)		29	30	31	32	33	34	35		224		Σ +(1n2)
n+29	n+30	n+31	n+32	n+33	n+34	n+35		Σ +(2n2)		36	37	38	39	40	41	42		273		Σ +(2n2)
n+36	n+37	n+38	n+39	n+40	n+41	n+42		Σ +(3n2)		43	44	45	46	47	48	49		322		Σ +(3n2)
								Σ										175		Σ
										154	161	168	175	182	189	196
Σ -(3n)	Σ -(2n)	Σ -(1n)	Σ	Σ +(1n)	Σ +(2n)	Σ +(3n)				Σ -(3n)	Σ -(2n)	Σ -(1n)	Σ	Σ +(1n)	Σ +(2n)	Σ +(3n)
								Σ										175		Σ
n-5	n-4	n-3	n-2	n-1	n	n-6		Σ -(3n2)		2	3	4	5	6	7	1		28		Σ -(3n2)
n+3	n+4	n+5	n+6	n+7	n+1	n+2		Σ -(2n2)		10	11	12	13	14	8	9		77		Σ -(2n2)
n+11	n+12	n+13	n+14	n+8	n+9	n+10		Σ -(1n2)		18	19	20	21	15	16	17		126		Σ -(1n2)
n+15	n+16	n+17	n+18	n+19	n+20	n+21		Σ		22	23	24	25	26	27	28		175		Σ
n+26	n+27	n+28	n+22	n+23	n+24	n+25		Σ +(1n2)		33	34	35	29	30	31	32		224		Σ +(1n2)
n+34	n+35	n+29	n+30	n+31	n+32	n+33		Σ +(2n2)		41	42	36	37	38	39	40		273		Σ +(2n2)
n+42	n+36	n+37	n+38	n+39	n+40	n+41		Σ +(3n2)		49	43	44	45	46	47	48		322		Σ +(3n2)
								Σ										175		Σ
										175	175	175	175	175	175	175
Σ	Σ	Σ	Σ	Σ	Σ	Σ				Σ	Σ	Σ	Σ	Σ	Σ	Σ
								Σ										175		Σ
n+3	n+12	n+17	n-2	n+23	n+32	n+41		Σ		10	19	24	5	30	39	48		175		Σ
n+11	n+16	n+28	n+6	n+31	n+40	n-6		Σ		18	23	35	13	38	47	1		175		Σ
n+15	n+27	n+29	n+14	n+39	n	n+2		Σ		22	34	36	21	46	7	9		175		Σ
n+26	n+35	n+37	n+18	n-1	n+1	n+10		Σ		33	42	44	25	6	8	17		175		Σ
n+34	n+36	n-3	n+22	n+7	n+9	n+21		Σ		41	43	4	29	14	16	28		175		Σ
n+42	n-4	n+5	n+30	n+8	n+20	n+25		Σ		49	3	12	37	15	27	32		175		Σ
n-5	n+4	n+13	n+38	n+19	n+24	n+33		Σ		2	11	20	45	26	31	40		175		Σ
								Σ										175		Σ
										175	175	175	175	175	175	175
Σ	Σ	Σ	Σ	Σ	Σ	Σ				Σ	Σ	Σ	Σ	Σ	Σ	Σ

---

 

Variations

The Mamzeris Method is remarkably flexible. By changing the shift directions, you can generate different magic squares for the same order:

• Left-shift + Up-shift (demonstrated above)
• Right-shift + Down-shift
• Left-shift + Down-shift
• Right-shift + Up-shift

Each direction combination produces a unique magic square while maintaining all magic properties.

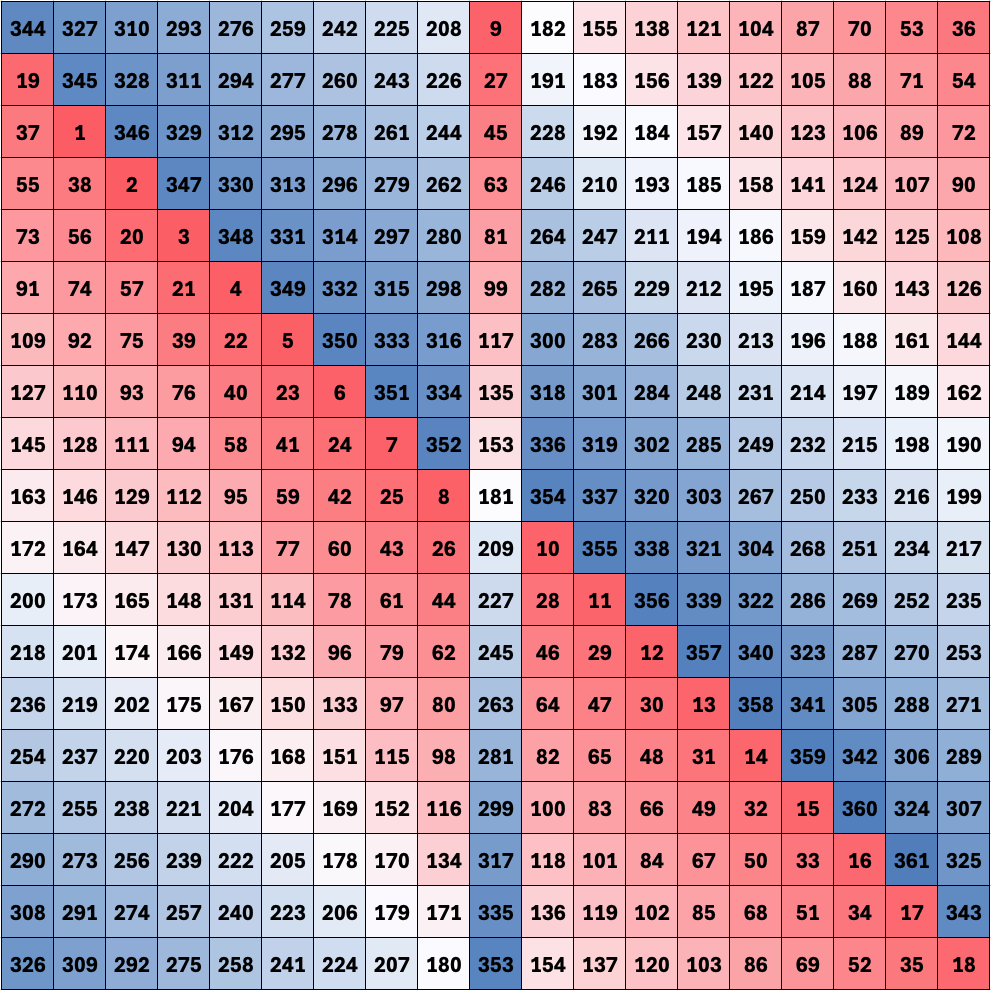
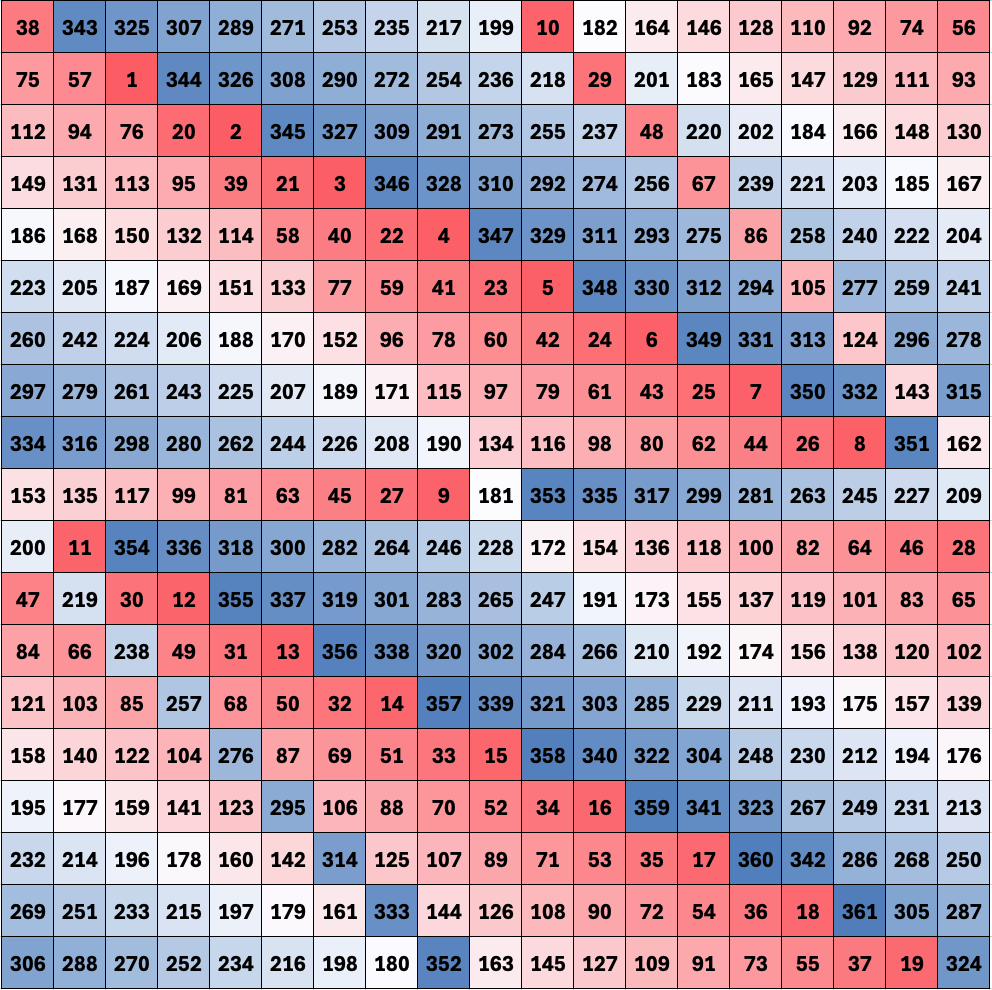
Below are four variations of a 19×19 associative magic square. Each uses the same two-pass technique with different shift directions. Cells are colour-coded by their numerical value to reveal the distinct patterns each variation creates.

---

Permutations

Beyond the four basic variations, each magic square has multiple permutations—different arrangements that preserve all magic properties. You can generate these by:

• Symmetrically shifting rows or columns
• Rotating the four quadrants
• Combining these transformations

Each permutation created by shifting rows can itself generate additional permutations through column shifts or quadrant rotations, and vice versa.

The Number of Permutations

The total number of permutations for each variation is given by:

$$\mathit{P}={\mathbf{2}}^{\mathit{n}-\mathbf{3}}\times {(\frac{\mathit{n}-\mathbf{1}}{\mathbf{2}}!)}^{\mathbf{2}}$$

Since the method allows four different variations, the total number of distinct magic squares for any odd order is 4×P.

For example, a 7×7 square yields 4 × 576 = 2,304 distinct magic squares.

Below are several examples (non-exhaustive) showing different permutations of a 7×7 magic square:

10 19 24 5 30 39 48 18 23 35 13 38 47 1 22 34 36 21 46 7 9 33 42 44 25 6 8 17 41 43 4 29 14 16 28 49 3 12 37 15 27 32 2 11 20 45 26 31 40

41 43 4 29 14 16 28 49 3 12 37 15 27 32 2 11 20 45 26 31 40 33 42 44 25 6 8 17 10 19 24 5 30 39 48 18 23 35 13 38 47 1 22 34 36 21 46 7 9

14 16 28 29 41 43 4 15 27 32 37 49 3 12 26 31 40 45 2 11 20 6 8 17 25 33 42 44 30 39 48 5 10 19 24 38 47 1 13 18 23 35 46 7 9 21 22 34 36

30 39 48 5 10 19 24 38 47 1 13 18 23 35 46 7 9 21 22 34 36 6 8 17 25 33 42 44 14 16 28 29 41 43 4 15 27 32 37 49 3 12 26 31 40 45 2 11 20

24 19 10 5 48 39 30 35 23 18 13 1 47 38 36 34 22 21 9 7 46 44 42 33 25 17 8 6 4 43 41 29 28 16 14 12 3 49 37 32 27 15 20 11 2 45 40 31 26

24 10 19 5 39 48 30 35 18 23 13 47 1 38 36 22 34 21 7 9 46 44 33 42 25 8 17 6 4 41 43 29 16 28 14 12 49 3 37 27 32 15 20 2 11 45 31 40 26

19 24 10 5 48 30 39 23 35 18 13 1 38 47 34 36 22 21 9 46 7 42 44 33 25 17 6 8 43 4 41 29 28 14 16 3 12 49 37 32 15 27 11 20 2 45 40 26 31

10 24 19 5 39 30 48 18 35 23 13 47 38 1 22 36 34 21 7 46 9 33 44 42 25 8 6 17 41 4 43 29 16 14 28 49 12 3 37 27 15 32 2 20 11 45 31 26 40

18 23 35 13 38 47 1 10 19 24 5 30 39 48 22 34 36 21 46 7 9 33 42 44 25 6 8 17 41 43 4 29 14 16 28 2 11 20 45 26 31 40 49 3 12 37 15 27 32

10 19 24 5 30 39 48 22 34 36 21 46 7 9 18 23 35 13 38 47 1 33 42 44 25 6 8 17 49 3 12 37 15 27 32 41 43 4 29 14 16 28 2 11 20 45 26 31 40

2 11 20 45 26 31 40 49 3 12 37 15 27 32 41 43 4 29 14 16 28 33 42 44 25 6 8 17 22 34 36 21 46 7 9 18 23 35 13 38 47 1 10 19 24 5 30 39 48

41 43 4 29 14 16 28 2 11 20 45 26 31 40 49 3 12 37 15 27 32 33 42 44 25 6 8 17 18 23 35 13 38 47 1 10 19 24 5 30 39 48 22 34 36 21 46 7 9

---

Rotations and Reflections

Each magic square can be rotated 90° in any direction to produce four different perspectives, all maintaining the magic properties.

 

4	3	8		8	1	6
9	5	1		3	5	7
2	7	6		4	9	2
6	7	2		2	9	4
1	5	9		7	5	3
8	3	4		6	1	8

 

Additionally, each magic square can be mirrored (reflected) horizontally or vertically to create four more variations. This means a 3×3 magic square has eight distinct orientations (4 rotations + 4 mirrored versions).

These rotation and reflection transformations preserve magic square properties and work for any magic square. Each transformation maintains the equal-sum property for all rows, columns, and diagonals.

---

For any comments or questions, please email me at contact@oddmagicsquares.com

Smaragdos (Marios) Mamzeris - Magic Squares